什么是星座图?
直观理解星座图
我们知道,信号的调制可以分为两类:模拟调制和数字调制。其中,模拟调制包含 AM、FM、PM 等;数字调制包含 PSK、FSK、MSK、QAM 等。
不论哪种调制方式,改变的无非是信号的三个变量:幅度、频率、相位。AM 会改变幅度,而 FM 和 PM 会改变相位角(FM 度量的是相位变化率)。因此,我们可以使用幅度和相位角来描述一种调制方式。极坐标图就是查看幅度和相位角的一种方式。
对于坐标系中的一点,相位角即为该点与水平轴所成的角度,幅度为该点与原点的距离。
在实际处理时,我们会使用 I/Q 图。
\(I\) 值即为该点横坐标,\(Q\) 值即为该点纵坐标。发送信号时,分别产生 \(I\) 信号和 \(Q\) 信号,将 \(Q\) 信号旋转 \(90\) 度后(使得两信号正交),合成发送。解调时,同样是把合成的信号分解为 \(I\) 信号和 \(Q\) 信号。如图所示(仅供示意)。
由上述内容我们可以总结出,对于任意编码方式,每种码元都是星座图上的一个点。发送时,根据码元的内容发送相应的点(也就是这个点表示的信号);接收时,根据收到的点得到码元。
为了在接收时更好的区分每个点的位置,我们需要使得任意两个点之间离得尽可能远。例如对于 BPSK,
而对于有 4 个点的 QPSK,则为
当然,由于干扰、噪声的存在,接收端收到的点并不总是在理想位置。下面三幅图是 6 bit 码元不同状态下的图,白色圆圈为理想位置,而红色点为接收到的位置。

因此,判断时会使用最大似然判决准则判断。换句话说,就是找距离最近的理想点。通常,我们使用划分决策边界的方法去寻找最近的理想点。例如,对于 2PSK,图中淡蓝色的区域即为 1 的决策区域。
再如上面提到的 QPSK,图中淡蓝色的区域即为 10 的决策区域。
然而,实际接收到的位置和理想位置不完全相同同,因此产生了角度误差和幅度误差。
数学理解星座图
设有 \(M\) 个定义在 \([0,T)\) 上的有限能量实信号 \(S=\left\{s_1(t),\cdots,s_M(t)\right\}\)。通过 Gram-Schmidt orthogonalization procedure,表示为 \(N\leq M\) 个 real orthonormal basis functions \(\left\{\phi_1(t),\cdots,\phi_N(t)\right\}\)。我们令这些 basis functions 组成的集合为 \(S\)。则有对于任意 \(s_i(t)\in S\),其可以写成
\[s_i(t)=\sum\limits_{j=1}^{N}s_{ij}\phi_j(t),0\leq t<T\]其中,
\[s_{ij}=\int_{0}^{T}s_i(t)\phi_j(t)\mathrm{d}t\]是将 \(s_i(t)\) 投影到 \(\phi_j(t)\) 上得到的实系数。
令 \(s_i=(s_{i1},\cdots,s_{iN})\in\mathbb{R}^N\),称其为 signal constellation point(信号星座点)。\(M\) 个信号星座点 \(\left\{s_1,\cdots,s_M\right\}\) 构成 signal constellation(信号星座图)。
显然,如果我们确定了所有的 \(\phi_j(t)\),那么就可以将 \(s_i(t)\) 和 \(s_i\) 互相转换。\(s_i(t)\) 用 \(s_i\) 表示被称为 signal space presentation,包含信号星座图的向量空间被称为 signal space。
换句人话说,就是把原来的一组向量用另外一组向量去表示。
我们在前文的所有星座图均为 \(s_i\in\mathbb{R}^2\) 上的星座图——通常的星座图也几乎都是二维的,也就是将所有的信号都用另外的两个信号去表示,这样可以使得发送和接收更加容易。
IQ 调制解调原理
前文提到,信号的收发是通过 \(I/Q\) 信号合成再拆解来进行的。具体是怎样的过程呢?
如图所示。在调制时,\(I\) 信号和 \(Q\) 信号合成为 \(I\cos{\omega_0t}-Q\sin{\omega_0t}\)。为了方便计算,\(I\) 信号和 \(Q\) 信号通常表示为复信号 \(I+jQ\)。于是,调制的过程相当于该信号乘以 \(e^{j\omega_0t}\) 得到的实部。即,
\[\Re{(I+jQ)e^{j\omega_0t}}=I\cos{\omega_0t}-Q\sin{\omega_0t}\]解调时,由于收到的信号是连续的,而我们需要的是离散的值,因此我们需要对一个周期内的信号积分求平均值。例如对于 \(I\) 信号。
\[I=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}s(t)\cos{\omega_0t}\mathrm{d}t\]其中,\(T\) 为周期。\(Q\) 信号的接收同理。
下面,我们利用 \(I/Q\) 调制解调原理来考察 QPSK。我们分别考虑下面四种四种码元所对应的 \(I/Q\) 坐标,计算信号的相位:
| 码元 | \(I\) | \(Q\) | \(s(t)\) 相位 |
|---|---|---|---|
00 | \(+A\) | \(+A\) | \(\frac{\pi}{4}\) |
01 | \(-A\) | \(+A\) | \(\frac{3\pi}{4}\) |
11 | \(-A\) | \(-A\) | \(\frac{5\pi}{4}\) |
10 | \(+A\) | \(-A\) | \(\frac{7\pi}{4}\) |
观察这四个 \(I/Q\) 坐标和相位,这正好是我们之前 QBSK 星座图的四个点的角度。
有一个问题是:为什么 11 对应 (-A,-A)、10 对应 (+A,-A),而不是按照顺序的 10 对应 (-A,-A)、11 对应 (+A,-A) 呢?这其实是格雷码在起作用。我们知道,对于一个码元,如果其传输过程中发生错误,那么最可能被误判为相邻的两个决策区域。例如对于上图的 11,其更可能被误判为 01 或者 10。在上图的情况下,无论哪一个码元传输出现错误,都只会影响到 1 个 bit。
然而,如果 10 对应 (-A,-A)、11 对应 (+A,-A),则如下图所示:
如果 11 错误的传为 00,或者 01 错误的传为了 10,则一下子要错 2 个 bit!
现在 QPSK 搞清楚了,那 BPSK 只有 2 个状态怎么办呢?很简单,只要 \(I\) 取 +A 和 -A,而 \(Q\) 置零就可以了。由此得到了 2 个点 (+A,0)、(-A,0)。
还有一个要解决的问题是,\(A\) 取值多少。我们前面说过,对于星座图,传输的其实是点的角度、到原点的距离。为了方便处理,我们通常会使距离设为整数。例如在 BPSK 中,\(A=1\);在 QPSK 中,我们使四个点落在单位圆上,得到 \(A=\frac{\sqrt{2}}{2}\)。
同理,对于 8PSK,我们使得 8 个点均匀分布在单位圆上即可:
如果点更多了,比如 16QAM 呢?如下图所示。
我们依然使用格雷码减小错误传输带来的影响。同时,为了使每个点尽可能隔开,其坐标取 \(-3A\)、\(-A\)、\(+A\)、\(+3A\)。
如果你仔细思考过,16QAM 还可以在原点放一点、周围围两个环,这样也可以满足每个点尽量隔开的要求。然而,这样做会产生一个问题:量化困难——即,无法很好地表示理想点坐标,造成运算处理的问题。
最后,我们考虑 MASK 的星座图。MASK 载波频率和相位为一常数,我们默认相位为 0。则点将会分布在 \(I\) 轴上。如图所示。
Matlab 模拟星座图
对于 QAM,我们以 64QAM 为例:
A = randi([0, 63], 1, 1000); % 16 进制,100 个码元
stem(A);
B = qammod(A, 64); % 64QAM 调制
scatterplot(B);
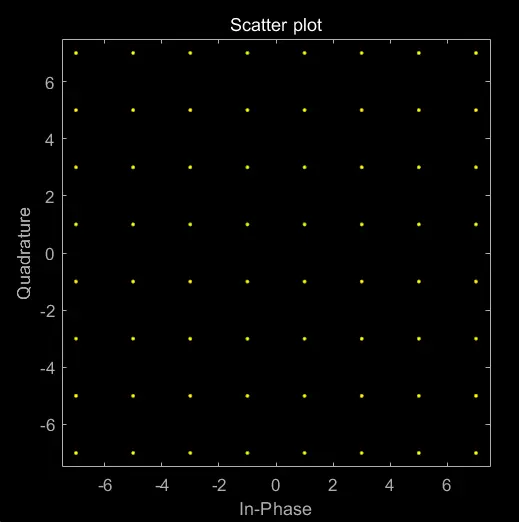
我们生成一张带有高斯白噪音的 64QAM 星座图:
M = 64;
k = log2(M);
data = randi([0 1],1000*k,1);
txSig = qammod(data,M,'InputType','bit','UnitAveragePower',true);
rxSig = awgn(txSig,25);
cd = comm.ConstellationDiagram('ShowReferenceConstellation',false);
cd(rxSig)
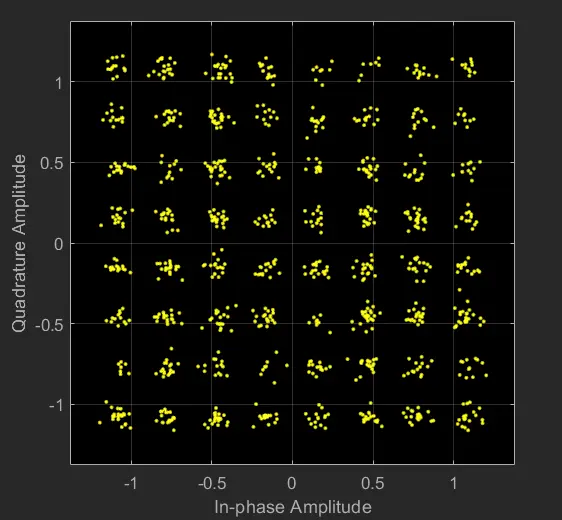
也可以进行解调
M = 64;
bitsPerSym = log2(M);
data = randi([0 1],1000*bitsPerSym,1);
txSig = qammod(data,M,'bin','InputType','bit','OutputDataType',numerictype(1,16,10));
z = qamdemod(txSig,M,'bin','OutputType','bit');
s = isequal(data,double(z))
同理,对于 PSK,我们以 4PSK 为例:
A = randi([0, 3], 1, 100); % 4 进制, 100 个码元
stem(A);
B = pskmod(A, 4, pi / 4); % 8PSK 调制, 初始相位为 pi / 4
scatterplot(B);
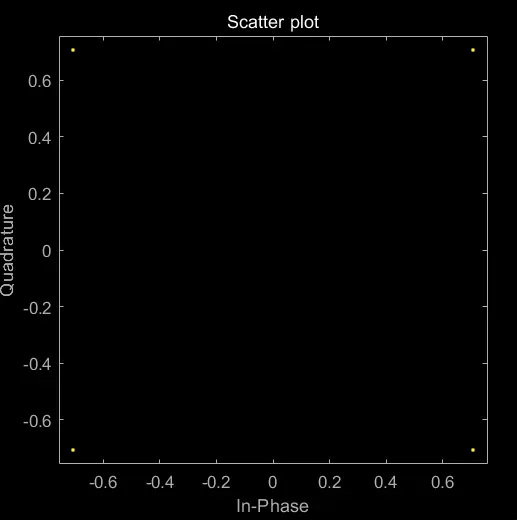













Comments