随机地图与开放世界永远令人着迷。从早期的 MineCraft 到现代的 No Man’s Sky,程序化生成的世界为玩家提供了无尽的探索和发现的机会。
在诸多程序化生成算法中,波函数坍缩(Wave Function Collapse, WFC)算法因其独特的生成方式和令人惊叹的结果而脱颖而出。下面就是我们使用波函数坍缩算法生成的图案:


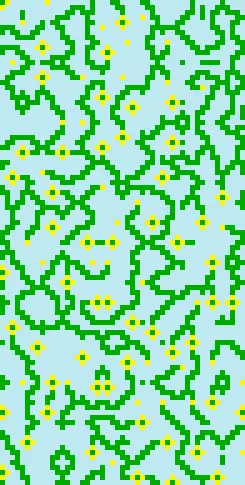





接下来,我们将深入探讨波函数坍缩算法的原理、实现以及应用。
请客吃饭的感悟
假设你是 The Family Guys 中国分 guy。你想要请你一大家子吃饭,大家需要围坐在一张大圆桌旁。但是位置有限,需要合理安排每个人的位置,以确保每个人都能愉快地交流:
- 你太爷爷是个冥顽不化的臭老九,他要是不坐主位,就会给你念之乎者也说你们是不肖子孙
- 你大伯是山东人,向来坚持女人不能上桌,需要让他尽量远离女人
- 你大舅舅是个男同,经常给你的两个妹夫暗送秋波,你需要把他们分开得远远的
- 你二舅舅是个花花公子,喜欢调戏你的小姨子,他们也不能坐一起
- 你小姨子极为泼辣,只有她老娘和老爹可以拿着鸡毛掸子才能压住她,所以需要让这三个人形成两面包夹芝士
- 你姑姑是从东北嫁过来的,爱吃地饺,需要把她安排到和大黄在一起
- 你自己是苏波宁,不配和上海来的表哥坐一起
- …

你头都要炸了,这该怎么安排是好!
忽然,你想起来在本博客里见过一个叫做波函数坍缩算法的东西。
在量子力学里,一个粒子在被观测前可能处于多个状态的叠加,一旦观测,它就会「坍缩」到某个确定状态。
类似地,在安排座位时:
-
第一步:叠加态 —— 刚开始,每个座位都处于「叠加态」,每个人理论上都可以坐在任何位置。就像薛定谔的猫,你姑姑既在主位也在次位,你大伯既挨着女人也远离女人,一切皆有可能。
-
第二步:观测坍缩 —— 你首先将太爷爷安排在了主位,这就是第一次”观测”。瞬间,这个决定像水池中的涟漪向外扩散,所有座位的「可能性」开始坍缩:
- 你小姨子不再能坐到主位旁边的两个位置 (可能性从 N 个减少到 N-2 个)
- 你太爷爷显然也不应该和大黄坐,所以你姑姑也不能坐在主位旁边 (又减少了 1 种可能)
- 其他位置依然是叠加态,但可能性空间变小了
-
第三步:连锁坍缩 —— 接下来你随机让大伯坐太爷爷左手边,这是第二次「观测」。又一波涟漪扩散:
- 大伯这边半张桌子都不能坐女人了 (半张桌子的女性可能性全部坍缩为 0)
- 由于你小姨子不能坐这半张桌子,她爹妈也不能坐这边 (连锁坍缩)
- 你大舅舅也不能坐这边,因为他要和你大伯分开 (继续坍缩)
-
第四步:强制坍缩 —— 算来算去,你发现大伯左手边的位置已经「过度坍缩」了——这个地儿的所有可能性只剩下一个:你自己!这就像量子态完全确定,再也没有其他选择。于是你就把自己安排在了那里。
-
第五步:递归坍缩 —— 你继续随机「观测」下一个人,每一次决定都会引发新的涟漪,不断压缩剩余位置的可能性空间,直到所有座位都从「叠加态」坍缩为「确定态」。
你顿悟了,这就是波函数坍缩算法!每一次决定都像一次量子观测,将无序的可能性逐步坍缩为有序的确定性,而约束条件就像物理定律,限制着坍缩的方向。
波函数坍缩算法
波函数坍缩算法(Wave Function Collapse, WFC)是一种基于约束满足问题(Constraint Satisfaction Problem, CSP)的程序化生成算法。它通过模拟量子力学中的波函数坍缩过程,生成符合特定规则的图案或结构。
与上文请客吃饭类似,波函数坍缩算法的核心思想是将生成过程视为一个约束满足问题。它通过以下步骤实现:
- 定义样本:首先,选择一个或多个样本图案,这些图案将作为生成新图案的基础
- 建立约束:分析样本图案,提取出其中的规则和约束。这些约束将指导新图案的生成过程
- 初始化状态:创建一个初始状态,通常是一个空白的网格或图像,每个单元格都处于「叠加态」,可以接受多种可能的值
- 观测与坍缩:随机选择一个单元格进行「观测」,根据约束条件确定该单元格的具体值,并更新周围单元格的可能性
- 重复迭代:不断重复观测与坍缩的过程,直到整个网格或图像都被填充为止
接下来,我们来一步一步地看看其实现。
样本与约束
首先是定义样本,其通常是一些具备一定重复特征和结构性的小图案,比如砖块、花纹、山脉等。下面是一些很经典的样本:

但这些样本还无法直接使用——总不能把一堆一模一样的图复制粘贴无数份吧!因此,我们需要先从其中提取出一些基本的 瓦片(Tile)。
例如,下面是一个 \(16 \times 16\) 的 Water 样本,我们从其中使用滑动窗口可以提取出 \(16 \times 16\) 个 \(3 \times 3\) 的瓦片:
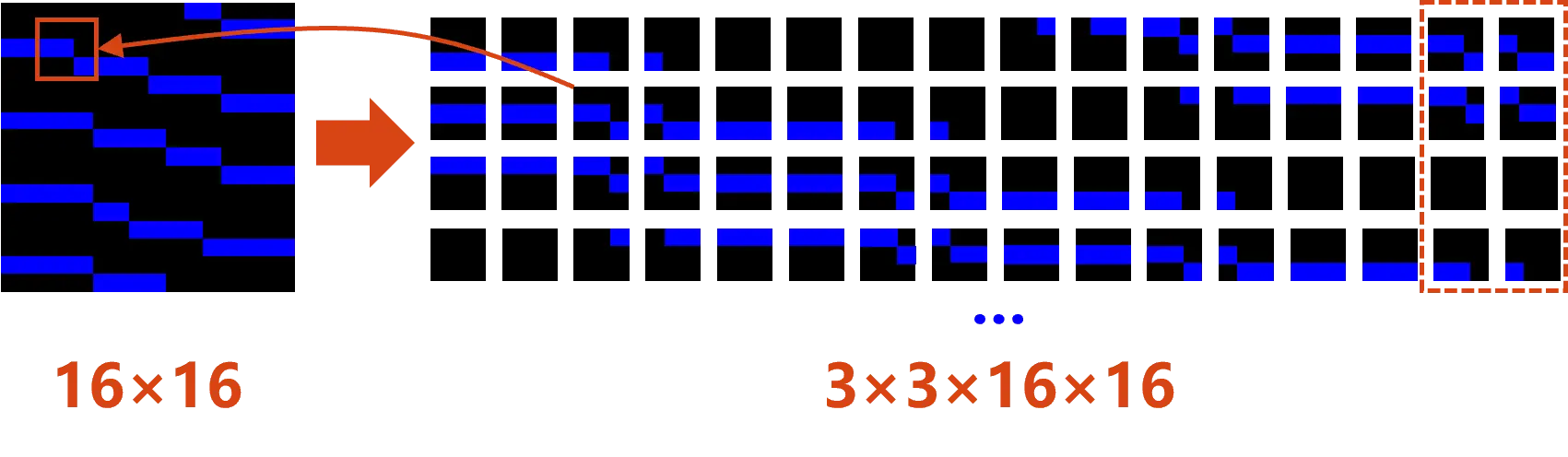
值得注意的是,边界处通过环绕连接(Wrap-around)来处理,这样可以确保瓦片在边界处也能正确匹配。
你也许已经发现,有很多瓦片是完全一样的。但我们并不需要去重,因为相同的瓦片数量恰恰体现了样本的「特征」,在后期生成时会影响概率分布。这就好像在很多大模型训练集中,「澳门银河」这个词出现的频率远高于「波函数坍缩」,所以生成时更容易出现前者。
当然,每个瓦片并不仅仅是它本身,它还可以旋转、翻转,对应共 \(8\) 种形态:

值得注意的是,并不是所有情况下都需要考虑变换,因为变换会带来不一样的邻接关系——或者更直观地讲,图像风格。例如 Water 在不变换和变换下生成的结果就完全不同:
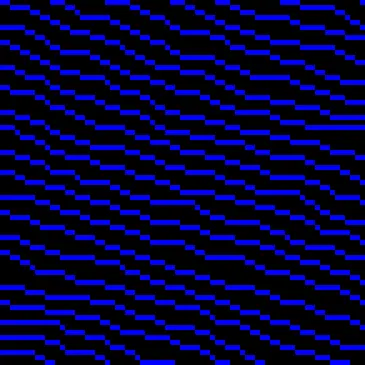

接下来便是建立约束了。每个瓦片的上下左右分别可以连接哪些瓦片,这些连接关系便是约束条件。
通常,我们认为,对应的边相同的瓦片可以连接在一起。例如,下面两个瓦片就是可以左右连接的:

我们可以通过遍历所有瓦片,记录每个瓦片在四个方向上可以连接的瓦片集合。
观测与坍缩
有了样本和约束,接下来便是核心的观测与坍缩过程了。
最开始,结果图像中的每个单元格都处于叠加态,意味着它们可以接受所有瓦片类型。我们可以用一个二维数组 possibleTiles 来表示每个单元格的可能瓦片集合:
每当我们随机选择一个单元格进行观测时,我们会从它的可能瓦片集合中随机选择一个瓦片,并将该单元格的状态坍缩为这个瓦片:
\[selectedTile[x][y] = random(possibleTiles[x][y])\]接着,我们需要更新周围单元格的可能瓦片集合,以确保它们仍然满足约束条件。假设我们选择了单元格 \((x, y)\) 并将其坍缩为瓦片 \(tile_k\),那么我们需要检查它的四个邻居:
\[\begin{align*} possibleTiles[x-1][y] =& possibleTiles[x-1][y] \\&\cap canConnect(tile_k, left) \\ possibleTiles[x+1][y] =& possibleTiles[x+1][y] \\&\cap canConnect(tile_k, right) \\ possibleTiles[x][y-1] =& possibleTiles[x][y-1] \\&\cap canConnect(tile_k, up) \\ possibleTiles[x][y+1] =& possibleTiles[x][y+1] \\&\cap canConnect(tile_k, down) \\ \end{align*}\]但是,这会带来连锁反应——当一个单元格的可能瓦片集合被更新后,它的邻居也可能需要更新,依此类推。为此,我们可以使用一个队列来跟踪需要更新的单元格:
- 初始化队列,将刚刚坍缩的单元格的邻居加入队列
- 当队列不为空时,取出一个单元格,更新它的可能瓦片集合
- 如果该单元格的可能瓦片集合发生变化,将它的邻居加入队列
- 重复步骤 2 和 3,直到队列为空
同时,我们还需要处理过度坍缩的情况——当一个单元格的可能瓦片集合变为空时,说明当前的选择导致了矛盾。此时,我们需要回溯到上一个状态,重新选择一个瓦片。
我们已经搞清楚了观测与坍缩的过程,但是,我们每次应该先观测哪个单元格呢?
这里,我们可以采用一种启发式的方法:每次选择可能瓦片集合最小的单元格进行观测。这种单元格的「熵」最小,这样可以最大化地减少不确定性,避免过早地陷入矛盾。
不过,为了防止陷入局部最优,我们可以在选择时引入一些随机性——在所有可能瓦片集合最小的单元格中,随机选择一个进行观测;或是在计算熵时加入一些噪声。
不断重复以上过程,直到所有单元格都被坍缩为具体的瓦片,或者无法继续进行,我们便得到了最终的生成结果!
实现
至此,我们便可以给出一个 Python 版本的波函数坍缩算法实现:
点击展开代码
"""
Wave Function Collapse (波函数坍缩) 图像生成器
这个程序使用 WFC 算法从输入图像中提取瓦片,并生成新的相似纹理图像。
算法通过约束传播确保相邻瓦片的边缘匹配,从而生成连贯的图像。
"""
import os
import random
import time
from datetime import datetime
from typing import Optional
import pygame
# ============================================================================
# 初始化
# ============================================================================
pygame.init()
MAX_INT: int = 2**31 - 1
# ============================================================================
# 配置类
# ============================================================================
class Config:
"""全局配置参数"""
# 瓦片来源设置
TILE_SOURCE_MODE: str = "folder" # "image" 或 "folder" - 从图像切割或从文件夹读取
TILE_FOLDER_PATH: str = "tiles" # 当模式为"folder"时,从此文件夹读取PNG文件作为瓦片
# 输入图像设置
ORIGINAL_IMG_PATH: str = "Water.png" # 源图像路径(仅在image模式下使用)
TILE_SIZE: int = 4 # 瓦片尺寸(像素),决定提取多大的图案块(仅在image模式下使用)
# 输出图像设置
OUTPUT_WIDTH: int = 24 # 输出图像宽度(瓦片数量)
OUTPUT_HEIGHT: int = 24 # 输出图像高度(瓦片数量)
SCALE: float = 1.0 # 显示缩放比例
# 瓦片变换设置
ALLOW_ROTATE: bool = True # 是否允许旋转瓦片(增加变化性)
ALLOW_FLIP: bool = True # 是否允许翻转瓦片(增加变化性)
# 显示设置
SHOW_GENERATION: bool = True # 是否实时显示生成过程
GENERATION_DELAY: float = 0.0001 # 每步之间的延迟(秒),0表示最快速度
# 输出设置
SAVE_OUTPUT: bool = True # 是否保存生成的图像
OUTPUT_DIR: str = "output" # 输出目录
# Pygame显示对象(延迟创建)
DISPLAY: pygame.Surface = None
# 确保输出尺寸为整数
Config.OUTPUT_WIDTH = int(Config.OUTPUT_WIDTH)
Config.OUTPUT_HEIGHT = int(Config.OUTPUT_HEIGHT)
# ============================================================================
# 瓦片类
# ============================================================================
class Tile:
"""
表示一个图像瓦片(图案块)
瓦片是从源图像中提取的小块图案,包含完整的像素数据和边缘信息。
边缘信息用于WFC算法中的瓦片匹配。
"""
def __init__(self, pixels: list[list[tuple]]):
"""
初始化瓦片
参数:
pixels: 2D数组 [y][x],每个元素是RGBA颜色元组
"""
self.pixels = pixels
self.height = len(pixels)
self.width = len(pixels[0]) if pixels else 0
# 提取四条边缘(用于匹配相邻瓦片)
self.edges = {
'up': tuple(pixels[0]), # 顶部边缘(第一行)
'right': tuple(row[-1] for row in pixels), # 右侧边缘(最后一列)
'down': tuple(pixels[-1]), # 底部边缘(最后一行)
'left': tuple(row[0] for row in pixels) # 左侧边缘(第一列)
}
# 创建Pygame Surface用于渲染
self.surface = pygame.Surface((self.width, self.height), pygame.SRCALPHA)
for y in range(self.height):
for x in range(self.width):
self.surface.set_at((x, y), pixels[y][x])
def rotate_90(self) -> 'Tile':
"""
顺时针旋转90度
返回:
旋转后的新瓦片对象
"""
new_pixels = [
[self.pixels[self.height - 1 - x][y] for x in range(self.height)]
for y in range(self.width)
]
return Tile(new_pixels)
def flip_horizontal(self) -> 'Tile':
"""
水平翻转(左右镜像)
返回:
翻转后的新瓦片对象
"""
new_pixels = [row[::-1] for row in self.pixels]
return Tile(new_pixels)
# ============================================================================
# 瓦片加载和处理函数
# ============================================================================
def load_tiles_from_image(image_path: str, tile_size: int) -> list[Tile]:
"""
使用滑动窗口从图像中提取瓦片
通过在源图像上滑动一个tile_size×tile_size的窗口,
每次移动1个像素,提取所有可能的图案块。
参数:
image_path: 源图像路径
tile_size: 瓦片尺寸(正方形边长)
返回:
提取的唯一瓦片列表
"""
img = pygame.image.load(image_path)
width, height = img.get_size()
tiles = []
tile_set = set() # 用于去重(避免重复的图案)
# 滑动窗口提取瓦片(步长为1像素)
for y in range(height - tile_size + 1):
for x in range(width - tile_size + 1):
# 提取tile_size × tile_size的像素块
pixels = []
for dy in range(tile_size):
row = []
for dx in range(tile_size):
color = img.get_at((x + dx, y + dy))
row.append((color.r, color.g, color.b, color.a))
pixels.append(row)
# 使用边缘元组作为唯一标识进行去重
tile = Tile(pixels)
edge_signature = (
tile.edges['up'],
tile.edges['right'],
tile.edges['down'],
tile.edges['left']
)
if edge_signature not in tile_set:
tile_set.add(edge_signature)
tiles.append(tile)
print(f"从图像提取了 {len(tiles)} 个唯一瓦片")
return tiles
def load_tiles_from_folder(folder_path: str) -> list[Tile]:
"""
从文件夹中加载所有PNG图像作为瓦片
读取指定文件夹中的所有PNG文件,每个文件作为一个瓦片。
所有瓦片必须具有相同的尺寸。
参数:
folder_path: 包含PNG瓦片文件的文件夹路径
返回:
加载的瓦片列表
"""
if not os.path.exists(folder_path):
raise FileNotFoundError(f"瓦片文件夹不存在: {folder_path}")
# 获取所有PNG文件
png_files = [f for f in os.listdir(folder_path) if f.lower().endswith('.png')]
if not png_files:
raise ValueError(f"文件夹中没有找到PNG文件: {folder_path}")
print(f"在文件夹 '{folder_path}' 中找到 {len(png_files)} 个PNG文件")
tiles = []
tile_set = set()
expected_size = None
for i, filename in enumerate(sorted(png_files)):
filepath = os.path.join(folder_path, filename)
try:
img = pygame.image.load(filepath)
width, height = img.get_size()
# 检查所有瓦片尺寸是否一致
if expected_size is None:
expected_size = (width, height)
print(f" 瓦片尺寸: {width}x{height} 像素")
elif (width, height) != expected_size:
print(f" ⚠ 跳过 '{filename}': 尺寸不匹配 ({width}x{height}, 期望 {expected_size[0]}x{expected_size[1]})")
continue
# 提取所有像素
pixels = []
for y in range(height):
row = []
for x in range(width):
color = img.get_at((x, y))
row.append((color.r, color.g, color.b, color.a))
pixels.append(row)
# 创建瓦片并去重
tile = Tile(pixels)
edge_signature = (
tile.edges['up'],
tile.edges['right'],
tile.edges['down'],
tile.edges['left']
)
if edge_signature not in tile_set:
tile_set.add(edge_signature)
tiles.append(tile)
print(f" ✓ 加载: {filename}")
else:
print(f" - 跳过重复: {filename}")
except Exception as e:
print(f" ✗ 加载失败 '{filename}': {e}")
continue
if not tiles:
raise ValueError("没有成功加载任何瓦片")
print(f"成功加载 {len(tiles)} 个唯一瓦片")
return tiles
def generate_tile_variants(
base_tiles: list[Tile],
allow_rotate: bool,
allow_flip: bool
) -> list[Tile]:
"""
生成瓦片的旋转和翻转变体
通过旋转和翻转原始瓦片,可以增加可用瓦片的数量和多样性,
从而生成更丰富的图案。
参数:
base_tiles: 原始瓦片列表
allow_rotate: 是否生成旋转变体(0°, 90°, 180°, 270°)
allow_flip: 是否生成翻转变体
返回:
包含所有变体的瓦片列表
"""
all_tiles = []
tile_set = set()
for tile in base_tiles:
variants = [tile]
# 生成旋转变体(90°, 180°, 270°)
if allow_rotate:
t = tile
for _ in range(3):
t = t.rotate_90()
variants.append(t)
# 生成翻转变体
if allow_flip:
flipped = tile.flip_horizontal()
variants.append(flipped)
# 翻转后的瓦片也可以旋转
if allow_rotate:
t = flipped
for _ in range(3):
t = t.rotate_90()
variants.append(t)
# 去重(有些变体可能相同,如对称图案)
for v in variants:
sig = (v.edges['up'], v.edges['right'], v.edges['down'], v.edges['left'])
if sig not in tile_set:
tile_set.add(sig)
all_tiles.append(v)
return all_tiles
def build_adjacency_rules(tiles: list[Tile]) -> dict:
"""
构建瓦片邻接规则
计算哪些瓦片可以相邻放置。两个瓦片可以相邻当且仅当
它们接触的边缘像素完全相同。
参数:
tiles: 所有可用的瓦片列表
返回:
邻接规则字典,格式为 {瓦片索引: {'up': [...], 'right': [...], ...}}
"""
rules = {
i: {'up': [], 'right': [], 'down': [], 'left': []}
for i in range(len(tiles))
}
# 对每一对瓦片,检查它们是否可以相邻
for i, tile1 in enumerate(tiles):
for j, tile2 in enumerate(tiles):
# 检查tile1的右边缘是否匹配tile2的左边缘
if tile1.edges['right'] == tile2.edges['left']:
rules[i]['right'].append(j)
rules[j]['left'].append(i)
# 检查tile1的下边缘是否匹配tile2的上边缘
if tile1.edges['down'] == tile2.edges['up']:
rules[i]['down'].append(j)
rules[j]['up'].append(i)
return rules
# ============================================================================
# WFC网格类
# ============================================================================
class WFCGrid:
"""
Wave Function Collapse 算法的核心网格类
维护一个网格,其中每个格子都有一组可能的瓦片选项。
通过不断"塌缩"(选择)格子的瓦片并传播约束,最终生成完整图像。
"""
def __init__(
self,
width: int,
height: int,
tiles: list[Tile],
rules: dict
):
"""
初始化WFC网格
参数:
width: 网格宽度(瓦片数量)
height: 网格高度(瓦片数量)
tiles: 可用的瓦片列表
rules: 瓦片邻接规则
"""
self.width = width
self.height = height
self.tiles = tiles
self.rules = rules
self.num_tiles = len(tiles)
# 每个格子的可能选项(初始时每个格子都可以是任意瓦片)
self.grid = [
[set(range(self.num_tiles)) for _ in range(width)]
for _ in range(height)
]
# 已确定的瓦片(None表示未确定)
self.collapsed = [
[None for _ in range(width)]
for _ in range(height)
]
def get_min_entropy_cell(self) -> Optional[tuple[int, int]]:
"""
找到熵最小的未塌缩格子
熵表示一个格子的不确定性(可能选项的数量)。
WFC算法优先选择熵最小的格子进行塌缩。
返回:
(x, y) 坐标,如果没有可用格子则返回None
"""
min_entropy = self.num_tiles + 1
candidates = []
for y in range(self.height):
for x in range(self.width):
if self.collapsed[y][x] is None:
entropy = len(self.grid[y][x])
if entropy == 0:
return None # 无解(矛盾)
if entropy < min_entropy:
min_entropy = entropy
candidates = [(x, y)]
elif entropy == min_entropy:
candidates.append((x, y))
# 在熵相同的格子中随机选择一个
return random.choice(candidates) if candidates else None
def collapse(self, x: int, y: int):
"""
塌缩指定格子(选择一个瓦片)
从该格子的可能选项中随机选择一个瓦片,
然后传播约束到相邻格子。
参数:
x: 格子的x坐标
y: 格子的y坐标
"""
if self.collapsed[y][x] is not None:
return # 已经塌缩过
if not self.grid[y][x]:
return # 无可用选项
# 随机选择一个瓦片
tile_idx = random.choice(list(self.grid[y][x]))
self.collapsed[y][x] = tile_idx
self.grid[y][x] = {tile_idx}
# 传播约束到相邻格子
self.propagate(x, y)
def propagate(self, start_x: int, start_y: int):
"""
约束传播算法
当一个格子被塌缩后,根据邻接规则更新相邻格子的可能选项。
这个过程会递归地传播到更远的格子。
参数:
start_x: 起始格子的x坐标
start_y: 起始格子的y坐标
"""
stack = [(start_x, start_y)]
while stack:
x, y = stack.pop()
# 检查四个方向的邻居
directions = [
(x, y - 1, 'up', 'down'), # 上方邻居
(x + 1, y, 'right', 'left'), # 右方邻居
(x, y + 1, 'down', 'up'), # 下方邻居
(x - 1, y, 'left', 'right') # 左方邻居
]
for nx, ny, my_dir, their_dir in directions:
# 检查邻居是否在网格范围内
if 0 <= nx < self.width and 0 <= ny < self.height:
if self.collapsed[ny][nx] is None:
# 计算邻居的有效选项
# (必须与当前格子的所有可能瓦片兼容)
valid_neighbors = set()
for tile_idx in self.grid[y][x]:
valid_neighbors.update(self.rules[tile_idx][my_dir])
# 更新邻居的选项(取交集)
old_options = self.grid[ny][nx]
new_options = old_options & valid_neighbors
# 如果选项发生变化,继续传播
if new_options != old_options:
self.grid[ny][nx] = new_options
if new_options: # 只有非空时才继续传播
stack.append((nx, ny))
def is_fully_collapsed(self) -> bool:
"""
检查是否所有格子都已塌缩
返回:
True表示生成完成,False表示还有未确定的格子
"""
for y in range(self.height):
for x in range(self.width):
if self.collapsed[y][x] is None:
return False
return True
def has_contradiction(self) -> bool:
"""
检查是否存在矛盾
矛盾指某个格子没有任何可用的瓦片选项,
这意味着当前的塌缩序列无法完成。
返回:
True表示存在矛盾,需要重新开始
"""
for y in range(self.height):
for x in range(self.width):
if self.collapsed[y][x] is None and not self.grid[y][x]:
return True
return False
# ============================================================================
# WFC算法执行函数
# ============================================================================
def run_wfc(
width: int,
height: int,
tiles: list[Tile],
rules: dict,
max_attempts: int = 10
) -> Optional[WFCGrid]:
"""
运行WFC算法(无显示)
参数:
width: 输出宽度(瓦片数量)
height: 输出高度(瓦片数量)
tiles: 可用瓦片列表
rules: 邻接规则
max_attempts: 最大尝试次数
返回:
成功时返回完成的网格,失败返回None
"""
for attempt in range(max_attempts):
print(f"\n尝试第 {attempt + 1} 次生成...")
grid = WFCGrid(width, height, tiles, rules)
steps = 0
while not grid.is_fully_collapsed():
# 检查是否出现矛盾
if grid.has_contradiction():
print(f" ✗ 发现矛盾(步骤 {steps}),重新开始")
break
# 找到熵最小的格子
cell = grid.get_min_entropy_cell()
if cell is None:
print(f" ✗ 无法继续(步骤 {steps}),重新开始")
break
# 塌缩该格子
x, y = cell
grid.collapse(x, y)
steps += 1
# 显示进度
if Config.SHOW_GENERATION and steps % 50 == 0:
uncollapsed = sum(
1 for row in grid.collapsed
for cell in row if cell is None
)
print(f" 进度: {steps} 步,剩余 {uncollapsed} 个格子")
time.sleep(Config.GENERATION_DELAY)
# 检查是否成功完成
if grid.is_fully_collapsed():
print(f"✓ 生成成功!共 {steps} 步")
return grid
print(f"\n⚠ {max_attempts} 次尝试后失败")
return None
def run_wfc_with_display(
width: int,
height: int,
tiles: list[Tile],
rules: dict,
display: pygame.Surface,
scale: float,
max_attempts: int = 10
) -> Optional[WFCGrid]:
"""
运行WFC算法,并实时显示生成过程
参数:
width: 输出宽度(瓦片数量)
height: 输出高度(瓦片数量)
tiles: 可用瓦片列表
rules: 邻接规则
display: Pygame显示窗口
scale: 显示缩放比例
max_attempts: 最大尝试次数
返回:
成功时返回完成的网格,失败返回None
"""
tile_size = tiles[0].width
overlap = 1
original_width = tile_size + (width - 1) * (tile_size - overlap)
original_height = tile_size + (height - 1) * (tile_size - overlap)
scaled_width = int(original_width * scale)
scaled_height = int(original_height * scale)
# 创建用于实时渲染的surface
render_surface = pygame.Surface((original_width, original_height), pygame.SRCALPHA)
clock = pygame.time.Clock()
for attempt in range(max_attempts):
print(f"\n尝试第 {attempt + 1} 次生成...")
grid = WFCGrid(width, height, tiles, rules)
render_surface.fill((50, 50, 50, 255)) # 灰色背景表示未确定的区域
steps = 0
while not grid.is_fully_collapsed():
# 处理pygame事件(允许用户关闭窗口)
for event in pygame.event.get():
if event.type == pygame.QUIT or \
(event.type == pygame.KEYDOWN and event.key == pygame.K_ESCAPE):
pygame.quit()
return None
# 检查是否出现矛盾
if grid.has_contradiction():
print(f" ✗ 发现矛盾(步骤 {steps}),重新开始")
break
# 找到熵最小的格子
cell = grid.get_min_entropy_cell()
if cell is None:
print(f" ✗ 无法继续(步骤 {steps}),重新开始")
break
# 塌缩该格子
x, y = cell
grid.collapse(x, y)
steps += 1
# 实时渲染刚刚塌缩的瓦片
if Config.SHOW_GENERATION:
tile_idx = grid.collapsed[y][x]
if tile_idx is not None:
tile = tiles[tile_idx]
pos_x = x * (tile_size - overlap)
pos_y = y * (tile_size - overlap)
# 绘制瓦片的所有像素
for ty in range(tile_size):
for tx in range(tile_size):
pixel = tile.pixels[ty][tx]
dest_x = pos_x + tx
dest_y = pos_y + ty
render_surface.set_at((dest_x, dest_y), pixel)
# 缩放并显示
scaled_surface = pygame.transform.scale(
render_surface,
(scaled_width, scaled_height)
)
display.fill((255, 255, 255))
display.blit(scaled_surface, (0, 0))
# 显示统计信息
if steps % 10 == 0:
uncollapsed = sum(
1 for row in grid.collapsed
for cell in row if cell is None
)
progress = (steps / (width * height)) * 100
pygame.display.set_caption(
f"WFC生成中... 步骤:{steps}/{width*height} "
f"进度:{progress:.1f}% 剩余:{uncollapsed}"
)
pygame.display.flip()
clock.tick(1000) # 限制最大帧率
if Config.GENERATION_DELAY > 0:
time.sleep(Config.GENERATION_DELAY)
# 检查是否成功完成
if grid.is_fully_collapsed():
print(f"✓ 生成成功!共 {steps} 步")
return grid
print(f"\n⚠ {max_attempts} 次尝试后失败")
return None
# ============================================================================
# 渲染和输出函数
# ============================================================================
def generate_output_filename() -> str:
"""
生成包含配置信息的输出文件名
文件名格式: 源图像名_瓦片大小_输出尺寸_变换_时间戳.png
例如: Water_t4_24x24_RF_20240101_120000.png
返回:
生成的文件名
"""
# 获取源图像名(不含扩展名)
source_name = os.path.splitext(os.path.basename(Config.ORIGINAL_IMG_PATH))[0]
# 生成时间戳
timestamp = datetime.now().strftime("%Y%m%d_%H%M%S")
# 构建变换描述
rotate_str = "R" if Config.ALLOW_ROTATE else ""
flip_str = "F" if Config.ALLOW_FLIP else ""
transform_str = rotate_str + flip_str if (rotate_str or flip_str) else "NoTrans"
# 构建完整文件名
filename = (
f"{source_name}_t{Config.TILE_SIZE}_"
f"{Config.OUTPUT_WIDTH}x{Config.OUTPUT_HEIGHT}_"
f"{transform_str}_{timestamp}.png"
)
return filename
def render_grid(grid: WFCGrid, tiles: list[Tile], scale: float) -> pygame.Surface:
"""
渲染网格到Surface,正确处理瓦片重叠
相邻瓦片共享边缘像素,确保生成的图像无缝连接。
参数:
grid: 完成的WFC网格
tiles: 瓦片列表
scale: 缩放比例
返回:
渲染并缩放后的Surface
"""
tile_size = tiles[0].width # 瓦片的完整尺寸
overlap = 1 # 相邻瓦片共享1个像素的边缘
# 计算原始图像尺寸
# 第一个瓦片占 tile_size 像素
# 后续每个瓦片增加 (tile_size - overlap) 像素
original_width = tile_size + (grid.width - 1) * (tile_size - overlap)
original_height = tile_size + (grid.height - 1) * (tile_size - overlap)
print(f" 瓦片尺寸: {tile_size}x{tile_size} 像素")
print(f" 网格尺寸: {grid.width}x{grid.height} 个瓦片")
print(f" 原始图像尺寸: {original_width}x{original_height} 像素")
print(f" 缩放后尺寸: {int(original_width * scale)}x{int(original_height * scale)} 像素")
# 创建渲染surface
surface = pygame.Surface((original_width, original_height), pygame.SRCALPHA)
# 渲染每个瓦片(相邻瓦片重叠绘制)
for y in range(grid.height):
for x in range(grid.width):
tile_idx = grid.collapsed[y][x]
if tile_idx is not None:
tile = tiles[tile_idx]
# 计算此瓦片在最终图像中的左上角位置
pos_x = x * (tile_size - overlap)
pos_y = y * (tile_size - overlap)
# 绘制完整的瓦片(所有像素)
for ty in range(tile_size):
for tx in range(tile_size):
pixel = tile.pixels[ty][tx]
dest_x = pos_x + tx
dest_y = pos_y + ty
surface.set_at((dest_x, dest_y), pixel)
# 缩放surface
scaled_width = int(original_width * scale)
scaled_height = int(original_height * scale)
scaled_surface = pygame.transform.scale(surface, (scaled_width, scaled_height))
return scaled_surface
# ============================================================================
# 主函数
# ============================================================================
def main():
"""
主程序入口
执行流程:
1. 加载并提取瓦片
2. 生成瓦片变体
3. 构建邻接规则
4. 创建显示窗口
5. 运行WFC算法
6. 渲染并保存结果
"""
print("=" * 60)
print("Wave Function Collapse - 图像生成器")
print("=" * 60)
start_time = time.time()
# ========================================================================
# 第1步: 加载瓦片
# ========================================================================
print(f"\n【第1步】加载瓦片...")
print(f" 模式: {Config.TILE_SOURCE_MODE}")
if Config.TILE_SOURCE_MODE == "folder":
# 从文件夹加载PNG瓦片
print(f" 文件夹路径: {Config.TILE_FOLDER_PATH}")
base_tiles = load_tiles_from_folder(Config.TILE_FOLDER_PATH)
elif Config.TILE_SOURCE_MODE == "image":
# 从图像切割瓦片
print(f" 源图像: {Config.ORIGINAL_IMG_PATH}")
print(f" 瓦片大小: {Config.TILE_SIZE}x{Config.TILE_SIZE}")
base_tiles = load_tiles_from_image(Config.ORIGINAL_IMG_PATH, Config.TILE_SIZE)
else:
raise ValueError(f"不支持的瓦片来源模式: {Config.TILE_SOURCE_MODE},请使用 'image' 或 'folder'")
# ========================================================================
# 第2步: 生成变体
# ========================================================================
print(f"\n【第2步】生成变体 (旋转={Config.ALLOW_ROTATE}, 翻转={Config.ALLOW_FLIP})...")
all_tiles = generate_tile_variants(
base_tiles,
Config.ALLOW_ROTATE,
Config.ALLOW_FLIP
)
print(f" 总共 {len(all_tiles)} 个瓦片")
# ========================================================================
# 第3步: 构建邻接规则
# ========================================================================
print("\n【第3步】构建邻接规则...")
rules = build_adjacency_rules(all_tiles)
# 统计规则
total_rules = sum(
len(r['up']) + len(r['right']) + len(r['down']) + len(r['left'])
for r in rules.values()
)
print(f" 总共 {total_rules} 条邻接规则")
# 显示前几个瓦片的规则统计
print("\n 前5个瓦片的邻接规则:")
for i in range(min(5, len(all_tiles))):
print(f" 瓦片 {i}: 上={len(rules[i]['up'])}, "
f"右={len(rules[i]['right'])}, "
f"下={len(rules[i]['down'])}, "
f"左={len(rules[i]['left'])}")
# ========================================================================
# 第4步: 创建显示窗口
# ========================================================================
tile_size = all_tiles[0].width
overlap = 1
original_width = tile_size + (Config.OUTPUT_WIDTH - 1) * (tile_size - overlap)
original_height = tile_size + (Config.OUTPUT_HEIGHT - 1) * (tile_size - overlap)
window_width = int(original_width * Config.SCALE)
window_height = int(original_height * Config.SCALE)
print(f"\n【第4步】创建窗口: {window_width}x{window_height} 像素")
Config.DISPLAY = pygame.display.set_mode((window_width, window_height))
pygame.display.set_caption("Wave Function Collapse - 初始化中...")
# ========================================================================
# 第5步: 运行WFC算法
# ========================================================================
print(f"\n【第5步】开始生成 {Config.OUTPUT_WIDTH}x{Config.OUTPUT_HEIGHT} 的图像...")
if Config.SHOW_GENERATION:
grid = run_wfc_with_display(
Config.OUTPUT_WIDTH,
Config.OUTPUT_HEIGHT,
all_tiles,
rules,
Config.DISPLAY,
Config.SCALE,
max_attempts=20
)
else:
grid = run_wfc(
Config.OUTPUT_WIDTH,
Config.OUTPUT_HEIGHT,
all_tiles,
rules,
max_attempts=20
)
# 检查生成是否成功
if grid is None:
print("\n❌ 生成失败!尝试调整参数:")
print(" - 减小输出尺寸")
print(" - 增大瓦片尺寸")
print(" - 启用旋转/翻转")
return
# ========================================================================
# 第6步: 渲染最终图像
# ========================================================================
print("\n【第6步】渲染最终图像...")
rendered = render_grid(grid, all_tiles, Config.SCALE)
# 保存图像
if Config.SAVE_OUTPUT:
# 确保输出目录存在
os.makedirs(Config.OUTPUT_DIR, exist_ok=True)
# 生成包含设置信息的文件名
filename = generate_output_filename()
output_path = os.path.join(Config.OUTPUT_DIR, filename)
pygame.image.save(rendered, output_path)
print(f" 图像已保存到: {output_path}")
# ========================================================================
# 显示总结信息
# ========================================================================
elapsed = time.time() - start_time
print(f"\n{'=' * 60}")
print(f"✓ 生成完成!总耗时: {elapsed:.2f}秒")
print(f"{'=' * 60}")
# ========================================================================
# 显示循环(等待用户关闭窗口)
# ========================================================================
pygame.display.set_caption("Wave Function Collapse - 完成!按ESC退出")
print("\n窗口已打开,按ESC或关闭窗口退出...")
clock = pygame.time.Clock()
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_ESCAPE:
running = False
Config.DISPLAY.fill((255, 255, 255))
Config.DISPLAY.blit(rendered, (0, 0))
pygame.display.flip()
clock.tick(30)
pygame.quit()
print("\n程序结束")
# ============================================================================
# 程序入口
# ============================================================================
if __name__ == "__main__":
main()
相关样本文件可以参考 GitHub - WaveFunctionCollapse。
讨论
算法优势
这个算法从效率角度来讲,算不上特别高效,但它的优势在于极高的自由度。
例如,我们上文是从一个样本图像中提取瓦片并生成新图像,但实际上,我们可以直接指定一组瓦片,以生成特定风格的图案:




同样的,对于游戏地图生成,我们还可以指定某处必须是某种瓦片(如水域),或是某处必须是空地等。这给了我们极大的灵活性。
从平面到立体
WFC 算法的另一个优势是,它并不局限于二维平面。我们可以将其扩展到三维,生成体素化的 3D 模型。
目前,已有很多类似的项目在做这件事,例如 Procedural Building Generation in Unity、Proc Skater 2016 等等。
对于三维情况,算法几乎不变,但瓦片变成了立方体,邻接规则也从四个方向变成了六个方向(上下左右前后)。这使得我们可以生成复杂的三维结构,例如建筑、地形等。在这种条件下,每次塌缩造成的影响会更大,更加容易出现矛盾,因此需要更强的瓦片集和更复杂的邻接规则。
Comments